Sind drei Punkte P1=[x1,y1],P2=[x2,y2],P3=[x3,y3] eines Dreiecks gegeben, so kann durch die Flächen A der Trapeze
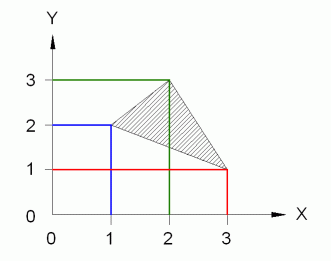
die Dreiecksfläche ausgedrückt werden: 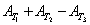
Die berühmte Gauß'sche Dreiecksformel lautet somit in der zusammengefassten Version
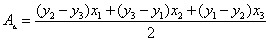
Erstellen wir jetzt daraus unsere Lisp-Funktion...
; Argumente
; #p1-#p3 = Punktkoordinanten '(1.50 2.80, 0.00)
; sexy coded by Rolf Wischnewski (www.cadmaro.de)
(defun :M-GaussAreaTriangle (#p1 #p2 #p3)
(* 0.5
(apply '+
(list (* (car #p1) (- (cadr #p2) (cadr #p3)))
(* (car #p2) (- (cadr #p3) (cadr #p1)))
(* (car #p3) (- (cadr #p1) (cadr #p2)))
)
)
)
)
Mit dieser Funktion können wir also die Fläche eines Dreiecks berechnen. Werden die Punkte im positiven Sinne durchlaufen, ist die Fläche negativ, sonst positiv.
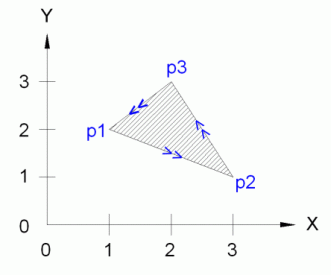
Schauen wir das Bild an und lassen uns mit der neuen Funktion die Fläche errechnen. Dabei übergeben wir die Punkte in der gegebenen Nummerierung
(setq p1 (getpoint)
p2 (getpoint)
p3 (getpoint)
)
(:M-GaussAreaTriangle p1 p2 p3) => 2049.56
Prüfen wir das Ergebnis mit der Autocad internen Flächenberechnung
(command "_area" "_o") => Fläche = 2049.5592, Umfang = 220.8448
Da die mit unserer Funktion errechnete Fläche positiv ist, wissen wir also, dass die Punkte gegen den Uhrzeigersinn laufen. Ändern wir die Laufrichtung ab
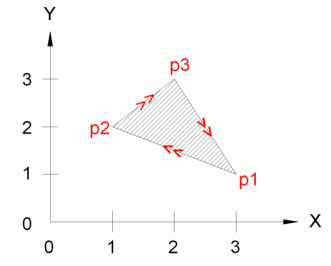
(:M-GaussAreaTriangle p1 p2 p3) => -2049.56
Aha, die Laufrichtung hat sich geändert, die Punkte laufen nun im Uhrzeigersinn und somit ist die Fläche negativ!
Beispiel
Ein Programm will durch klicken des Anwenders die Seite einer Linie bestimmen um dort eine Kopie der Linie zu erstellen. Da wir in der Programmierung nichts "sehen", müssen wir also auf mathematischen Weg die Seite bestimmen...los geht's
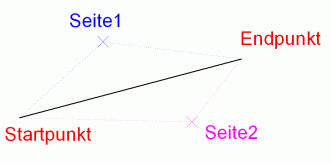
Wir haben eine Linie dessen Startpunkt und Endpunkt wir auslesen
(cond ((setq LinienObjekt (entsel "Bitte Linie auswählen..."))
(setq Startpunkt (cdr (assoc 10 (entget (car LinienObjekt))))
Endpunkt (cdr (assoc 11 (entget (car LinienObjekt))))
)
)
)
Als nächsten Schritt fragt das Programm nach einer Seite (für unser Beispiel nehmen wir beide Seiten auf)...
(setq Seite1 (getpoint)
Seite2 (getpoint)
)
Jetzt haben wir alle relevanten Daten und können nun mit Hilfe unserer Funktion die Seite bestimmen...
Seite1 : (setq Flaeche1 (:M-GaussAreaTriangle Startpunkt Endpunkt Seite1)) => 2599.25
Seite2 : (setq Flaeche2 (:M-GaussAreaTriangle Startpunkt Endpunkt Seite2)) => -2416.07
Erstellung eine Linienkopie auf der 1. Seite (Seite1) mit Hilfe der ActiveX Schnittstelle
(vl-load-com)
(vla-offset
(vlax-ename->vla-object (car LinienObjekt))
(if (minusp Flaeche1)
-10
10
)
)
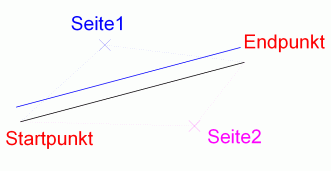
Erstellung eine Linienkopie auf der 2. Seite (Seite2) mit Hilfe der ActiveX Schnittstelle
(vl-load-com)
(vla-offset
(vlax-ename->vla-object (car LinienObjekt))
(if (minusp Flaeche2)
-10
10
)
)
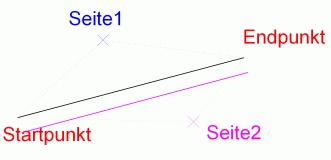
Wie wir sehen, wird die neue Linie immer auf der Seite angegeben, die der Anwender durch klicken bestimmt hat.
Zum Schluss prüfen wir durch Vertauschen des Start- und Endpunktes ob es auch andersherum klappt, die Linie also einen andere Laufrichtung hat.
(setq Startpunkt (cdr (assoc 11 (entget (car LinienObjekt)))) ;_ ist eigentlich der Endpunkt
Endpunkt (cdr (assoc 10 (entget (car LinienObjekt)))) ;_ ist eigentlich der Startpunkt
)
Probieren wir unser Offset nochmal aus...und ?
Yep, auch wenn die Linie eine andere Laufrichtung hat, wird mit der Hilfe der Gauß'schen Dreiecksformel die richtige Seite für den Betrachter ermittelt.
Mit freundlicher Genehmigung von Rolf Wischnewski. Originalbeitrag im Februar 2006, CADmaro.de
