Wie kann man einfach prüfen, ob 3 Punkte kollinear sind. Kollinear heisst, dass 3 oder mehr Punkte auf einer Geraden liegen. Eine Möglichkeit ist die hier bereits vorgestellte Dreiecksformel nach Gauss. Werden 3 Punkte übergeben und diese Punkte liegen auf einer Geraden, so ist die Fläche 0!
Eine andere Möglichkeit in der linearen Algebra ist die Vektorberechnung unter Verwendung des Vektorprodukts. Mit Hilfe des Vektorprodukts ist es unter anderem möglich zu prüfen, ob 2 Vektoren parallel zueinander d.h. linear abhängig (kollinear) sind. Sind 2 Vektoren linear abhängig (kollinear), dann ist das Vektorprodukt 0 (0.0 0.0 0.0).
Was ist ein Vektor?
Ein Vektor ist eine Liste von Zahlen. Damit können mehrere Zahlen zu einem mathematischen Objekt zusammengefasst werden. Ein Vektor kann - ebenso wie eine Zahl - einen Buchstaben oder ein anderes Symbol als Namen bekommen. Vektoren, die zwei Eintragungen besitzen, heißen zweikomponentige, auch zweidimensionale, Vektoren. Vektoren, die drei Eintragungen besitzen, heißen demnach dreikomponentige, auch dreidimensionale Vektoren.
In diesem Artikel verwenden wir nur dreikomponentige Vektoren. Im Internet gibt es hierzu eine Menge mehr an Informationen. Einfach mal bei diversen Universität's- und Mathematikforen nachstöbern.
1. Schritt - Segment in Vektoren
Ein Segment besteht aus 2 Punktkoordinaten.
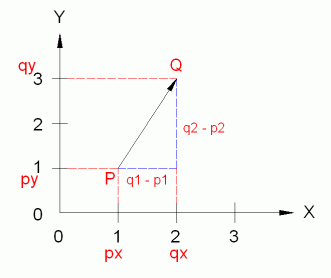
Um einen Vektor zu erhalten subtrahieren wir P von Q. Diese Art von Vektoren heissen Verbindungsvektoren und werden mathematisch so beschrieben:
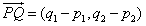
Jetzt können wir uns eine Funktion schreiben, die aus einem Segment einen Verbindungsvektor zurückgibt. Unsere Funktion benötigt hierzu zwei 3D-Punkte als Argumente.
; Argumente: 2 3D-Punkte
; Rückgabe : Verbindungsvektor
(defun :M-GetVector (#p1 #p2)
(mapcar '- #p1 #p2)
)
Aufruf:
(:M-GetVector (getpoint) (getpoint))
=> (-128.583 -68.9569 0.0)
2. Schritt - Vektorprodukt
Das Vektorprodukt ist nur für dreidimensionale (räumliche) Vektoren definiert. Im Unterschied zum Skalarprodukt macht es aus zwei Vektoren einen dritten (daher auch sein Name). Seien a und b zwei räumliche Vektoren, dann definieren wir einen Vektor namens a ^ b unter anderem wie folgt: a ^ b ist genau dann 0, wenn a und b zueinander parallel sind, denn nur dann ist der Flächeninhalt des von ihnen aufgespannten Parallelogramms gleich 0, d.h. sie sind linear abhängig (kollinear).
Hier nun die Formel...
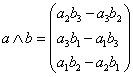
; Argumente : 2 dreikomponentige Vektoren
; Rückgabe : Vektor (Vektorprodukt)
(defun :M-VectorProduct (#v1 #v2)
(list (- (* (cadr #v1) (caddr #v2)) (* (caddr #v1) (cadr #v2)))
(- (* (caddr #v1) (car #v2)) (* (car #v1) (caddr #v2)))
(- (* (car #v1) (cadr #v2)) (* (cadr #v1) (car #v2)))
)
)
3. Schritt - Funktion zur Ermittlung von kollinearen Punkten
Das ist nun keine große Kunst mehr.
; Argumente: 3 3D-Punkte
; Rückgabe : True= kollinear, sonst nil
(defun :M-Collinear (#p1 #p2 #p3 /)
(equal '(0.0 0.0 0.0)
(:M-VectorProduct
(:M-GetVector #p1 #p2)
(:M-GetVector #p1 #p3)
)
1.0e-010
)
)
Falls 3 Punkte auf einer Geraden liegen gibt die Funktion ein True zurück, ansonsten nil. Durch equal können wir einen Genauigkeitswert vergeben. Hier in unserer Funktion enspricht 1.0e-010 = 0.0000000001
Beispiel:
(:M-Collinear '(0.0 0.0 0.0) '(3.15 0.0 0.0) '(2.0 0.0 0.0))
=> T
Zum Schluss überlegen wir, wie wir aus einer Liste mit Punktkoordinaten prüfen können, ob alle Punkte zueinander Kollinear sind.
; Argument : #lst-of-points = Liste mit Punktkoordinaten
; sexy coded by Rolf Wischnewski (www.cadmaro.de)
(defun :M-Collinear>L (#lst-of-points / 1stVector RetVal)
(setq 1stVector
(:M-GetVector (car #lst-of-points) (cadr #lst-of-points))
)
(while
(and (cddr #lst-of-points)
(setq
RetVal (equal
'(0.0 0.0 0.0)
(:M-VectorProduct
1stVector
(:M-GetVector
(car (setq #lst-of-points (cdr #lst-of-points)))
(cadr #lst-of-points)
)
)
1.0e-010
)
)
)
)
RetVal
)
(:M-Collinear>L
'((0.0 0.0 0.0)
(2.0 0.0 0.0)
(1.0 0.0 0.0)
(0.107322 0.0 0.0)
(0.37325 0.0 0.0)
(1.78599 0.0 0.0)
(1.52338 0.0 0.0)
(0.702335 0.0 0.0)
(1.25081 0.0 0.0)
(1.89236 0.0 0.0)
)
)
=> T
(:M-Collinear>L
'((0.0 0.0 0.0)
(2.0 0.0 0.0)
(1.0 0.0 0.0)
(0.107322 0.0 0.0)
(0.37325 1.0 0.0);_ hier ist die Y-Koordinate verändert
(1.78599 0.0 0.0)
(1.52338 0.0 0.0)
(0.702335 0.0 0.0)
(1.25081 0.0 0.0)
(1.89236 0.0 0.0)
)
)
=> nil
Wie funktioniert's?
Als erstes entneme ich aus einer Punkteliste die ersten zwei Punkte und wandle diese in einen Vektor um, den ich schließlich an ein Symbol binde (Variable: 1stVector). Mit Hilfe der While Schleife iteriere ich so lange durch die Liste (ab der 3. Stelle) bis, entweder die Liste keinen dritten Eintrag mehr enthält oder die equal Funktion ein nil zurückgibt, was bedeutet, dass das Vektorprodukt ungleich (0.0 0.0 0.0) ist. Durch die While Schleife habe ich den Vorteil, dass ich nicht durch die ganze Liste iterieren muss. Sie bricht ab, sobald ein Punkt nicht mehr Kollinear ist.
Mit freundlicher Genehmigung von Rolf Wischnewski. Originalbeitrag im Februar 2006, CADmaro.de
